Naught Product Property

The "Zero Production Property" says that:

If a × b = 0 and then a = 0 or b = 0
(or both a=0 and b=0)

Information technology tin aid us solve equations:

Example: Solve (10−v)(x−three) = 0

The "Aught Product Property" says:

If(x−five)(ten−3) = 0  and then (x−5) = 0 or (x−3) = 0

At present nosotros just solve each of those:

For (ten−v) = 0 we get 10 = 5

For (x−3) = 0 we become ten = 3

And the solutions are:

x = 5, or x = 3

Hither information technology is on a graph:

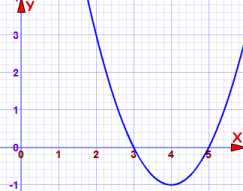
(x-5)(x-3) = 0 graph
y=0 when ten=3 or x=5

Standard Form of an Equation

Sometimes nosotros tin can solve an equation past putting it into Standard Class and and then using the Zero Product Property:

The "Standard Course" of an equation is:

(some expression) = 0

In other words, "= 0" is on the right, and everything else is on the left.

Example: Put x2 = 7 into Standard Form

Answer:

x2 − 7 = 0

Standard Form and the Zero Product Property

So allow's try it out:

Example: Solve 5(x+3) = 5x(ten+3)

It is tempting to dissever by (10+3), only that is dividing by zero when ten = −iii

So instead we can use "Standard Class":

v(ten+iii) − 5x(x+iii) = 0

Which can exist simplified to:

(five−5x)(x+3) = 0

five(1−x)(ten+3) = 0

And then the "Zero Product Property" says:

(1−x) = 0, or (x+3) = 0

And the solutions are:

x = 1, or x = −3

And another example:

Example: Solve xthree = 25x

It is tempting to divide by ten, only that is dividing by zero when x = 0

Then allow's use Standard Form and the Zero Product Property.

Bring all to the left mitt side:

xiii − 25x = 0

Factor out x:

x(x2 − 25) = 0

tentwo − 25 is a departure of squares, and tin be factored into (x − 5)(10 + v):

x(10 − 5)(x + 5) = 0

At present nosotros tin see three possible ways it could terminate up every bit zero:

x = 0, or x = five, or x = −v